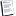
I got it solved for you Shaun, as follows is the calcs.

Horse 1 ($4.38)

As we've stated before this is the simple part, you want a $100 liability so to work out what your profit is if Horse 1 loses is simply $100/($4.38-1) which equals $29.58

Horse 2 ($4.88) & Horse 3 ($5.70)

First step is work out %'s of each horse:

$4.88 = 1/4.88 = 0.204918
$5.70 = 1/5.70 = 0.175439

Next you sum these for 0.380357 which you then convert back to odds to give the combined odds of these runners:

1/0.380357 = 2.629112

As you want your combined liability of these two to equal the profit from Horse 1 you can work out the combined profit achieved by these runners which is simply:

29.5858/(2.629112 - 1) = 18.1607

So now that you have the target profit of these two Horses to ensure a $29.5858 liability you just have to split between the two based on their odds, so:

0.204918 / 0.380357 = 0.538752 * 18.1607 = 9.784118 Profit target for Horse 2

0.175439 / 0.380357 = 0.461248 * 18.1607 = 8.376578 Profit target for Horse 3

Now that you have the profit targets for each individual horse so that they combined break even if either of them lose, you simply work backwards to find their liabilities:

Horse 2 = 9.784118 * (4.88 - 1) = 37.96238

Horse 3 = 8.376578 * (5.70 - 1) = 39.36992

Therefore your returns based on each horse winning =

Horse 1 = -$81.84
Horse 2 = $0
Horse 3 = $0

Any other horse = $47.75

I hope all of the above makes sense, if not let me know and I can provide the example in excel format so you can see all the equations working.